L
likearock111
Guest
Hey all,
I figured that posting an easy how-to for the electronics behind making your own LED turn signals might be helpful to some people. I'm trying to make this post a good balance between simple, educational, and fun to build. To all you Electrical Engineering buffs out there, be forewarned that the circuit I drew up to share is a little overly simplistic (couple optional resistors missing, etc.), but it will work just fine for our purposes. Also, I'd just like to say that this is pretty basic and has probably all been done before by someone else, so I'd just like to let you know that it's not very original. But it does work great!
Hope someone can get some benefit out of this! Feel free to question away.
---------------------------------------------
How to Build your own LED Turn Signals
You will need:
- 2x medium-sized 12V LED modules. I got mine at AutoZone (kind of like this one), but you can find them all over the net. What you're looking for is a red or yellow housing that contains maybe 5-10 LEDs. There should be 2 wires sticking out of it. Just about any type that fit this description will work.
- A means for powering your LEDs. For this how-to, I'm assuming that you have a 12V SLA battery like I do. This setup should also work for 6V systems, although I've not tried a "white wire" setup before.
- 2x N-channel MOSFETS with sufficient current and voltage capabilities. I used International Rectifier's IRLML2803 (datasheet here), but I wouldn't recommend them, for reasons I'll explain later. If you don't know what MOSFETs are, don't worry. We'll get to that later, and they're easy to work with - I promise.
- 1x astable multivibrator or oscillator. I used Texas Instruments' CD4047BE in astable mode (datasheet here), but a standard 555 timer could also be modified to fit the system. Again, don't let the terminology freak you out. We'll clear all this up in a bit.
- Wire, solder, soldering iron, multimeter.
- 2x Dual-pole, Dual-throw switches, one resistor, and one capacitor (details below). RadioShack has them.
------------
So, I guess now would be the time to dive in. First of all, let's think about what we're trying to do. What I was shooting for were two tail lights that, when connected to the battery, were always on, except when I wanted to turn. When turning, I wanted to be able to flip a switch and have one of the two lights go from always on to flashing.
That means that we need to be applying 12V to each of the LEDs continuously, then throw a switch and apply 12V to one of the LEDs intermittently and the other continuously.
So how can you do this? Well, imagine two parallel ways of powering the LEDs. One way is 12V constant, and the other way is 12V/0V intermittently. The switch changes which of the two powering methods the LED is connected to. Now would be a good time to bring up the circuit.
Astable Multivibrator
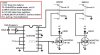
In the lower left part of the circuit diagram, there is a block (an "integrated circuit") in the lower left labeled "CD4047BE". It's called a "multivibrator," and it is currently set up to run in "astable" mode. Now, this is really just a bunch of fancy-schmancy lingo that EE's came up with to make their jobs sound complicated . All it really means is that if you watched the voltage at pin number 10, the voltage would go from 0V (ground), to 12V (high), then back to 0V, then back to 12V... for as long as you have it set up this way and are giving it power. That's why I labeled it with an up-down square wave. It's called "astable", because it never stays at the same voltage - it keeps on switching back and forth.
. All it really means is that if you watched the voltage at pin number 10, the voltage would go from 0V (ground), to 12V (high), then back to 0V, then back to 12V... for as long as you have it set up this way and are giving it power. That's why I labeled it with an up-down square wave. It's called "astable", because it never stays at the same voltage - it keeps on switching back and forth.
So what determines how fast the voltage goes back and forth? Well, basically, there are two circuit components - a resistor (actually a potentiometer in the diagram) and a capacitor - that determine the frequency at which the voltage at pin 10 goes back and forth. The capacitor is going between pins 1 and 3, and the potentiometer is going between pins 2 and 3 in the diagram.
So how do you actually control the flashing frequency? Well, resistors and capacitors have certain values associated with them that quantify how they will behave if you put them in a circuit. Let's say that R = resistance and C = capacitance. In order to get a certain flashing frequency, you need 1/(R*C) to be, say, F (for frequency). You could have R be really big and C be really small, R be really small and C be really big, or R and C both be medium-sized, and you could get the exact same F. Therefore, the way the diagram is set up, you can vary R from very small (a few ohms) to somewhat large (3 kilo-ohms), and C is fixed at 100 uF. This allows you to dial the frequency value in by changing the R through twisting the knob on the potentiometer. For you circuits-minded people out there, this is on page 3-135 of the CD4047BE datasheet linked to above.
The other two most important pins on this integrated circuit are pins 7 and 14. 7 is where you attach 0V (GND), and 14 is where you connect +V (12V in this case).
CD4047BE Pin Recap
Pins 1-3: Attach resistor/capacitor to determine flashing frequency
Pins 4-6: Connect to V+, to "tell" the IC you want it to run in astable mode
Pin 7: This is the GND pin of the IC, where you should connect 0V
Pins 8-9: Connect to GND to "tell" the IC you want it to run in astable mode
Pin 10: This is the output of the chip, going back and forth between 0V and 12 V
Pin 11: Do nothing
Pin 12: Connect to GND to "tell" the IC you want it to run in astable mode
Pin 13: Do nothing
Pin 14: This is the V+ pin, where you should connect 12V
I get all of my circuit components from Digikey or Jameco. I provided Digikey links above.
LED Current Draw
You may be wondering why, now that we have a component that will output a flashing 12V/0V/12V/0V signal, we don't just hook 'er up to the LEDs and go. Well, as it turns out, the astable multivibrator isn't capable of actually powering the LEDs directly. In circuit-speak, the astable multivibrator isn't capable of sourcing enough current to operate the LEDs, even though its output voltage is just right.
Now I'm sure you're thinking, "So HOW much current do you actually NEED to power the LEDs?" Good question. We need to figure that out now.
We need to figure that out now.
First, put your multimeter on the "mA DC" or "A DC" setting. To be safe, start with the highest current setting your multimeter has and work your way down. Also, be sure your multimeter probes are plugged into the correct holes (this is really easy to switch up). Black goes into "COM" or "GND", and red goes into "mA" or "A".
Next, attach the red wire (or positive lead) of your LED module to the red (+12V) terminal of the battery. Attach the black wire (or negative lead) of your LED module to the red probe of your multimeter. Attach the black probe of your multimeter to the black (0V) terminal of the battery. Your LED should light up, and your multimeter should be displaying the amount of current going through it. This is the amount of current you should pay attention to when selecting your MOSFETs. Mine turned out to be 60 mA for each of the two 5-LED light modules I went with.
N-Channel MOSFETs
So what the heck is an N-channel MOSFET? Well, for the sake of this project, its just a glorified switch. That's it. I swear. The only thing special about this switch is that instead of controlling it with a physical lever or pushbutton, you can control it with voltage! So, if you give it a high voltage (but not toooo high), it "closes the connection" (current can flow through it freely), and if you give it a voltage right around 0V (GND), it "opens the connection" (no current can flow through it). Unlike a relay, nothing mechanically opens and closes. Instead, the voltage applied to it changes the conduction properties of the materials inside. No moving parts? Even better!
Because we can control this "switch" with a voltage, we will use the output of the astable multivibrator mentioned previously to control its operation!
A MOSFET has three connections (terminals): a Gate, Drain, and Source (labeled with G, D, and S in the diagram). The gate is the pin where you apply a voltage to control the switch. As a result, we'll eventually hook pin 10 of the astable multivibrator directly to the gate of both MOSFETs (<EE's grit teeth in anguish> ). When the "switch" is closed, current is allowed to flow from the drain to the source. Therefore, we'll put the drain-to-source path of one MOSFET in the current path for one of the LED modules. Then when the astable multivibrator outputs 0V, the LEDs will be "off", and when the astable multivibrator outputs 12V, the LEDs will be "on".
). When the "switch" is closed, current is allowed to flow from the drain to the source. Therefore, we'll put the drain-to-source path of one MOSFET in the current path for one of the LED modules. Then when the astable multivibrator outputs 0V, the LEDs will be "off", and when the astable multivibrator outputs 12V, the LEDs will be "on".
As I said earlier, I picked International Rectifier's IRLML2803, due to availability. I wouldn't recommend this particular MOSFET to anyone, because it is a surface mount component (basically, it's super-tiny and kind of hard to hand-solder to without good equipment). Therefore, you'll need to pick yourself out a couple. Here is what to look for:
1. Get one in a nice big package. Any of the through-hole form factors listed on this website (down at the bottom) should work great for you. This will make soldering sooo much easier!
2. Pick one that can handle the current levels you need. Remember that LED module current measurement we did earlier? That's the one. Your MOSFET needs to be able to have a "continuous drain current" of at least 120% of the measured current. This is often labeled as "Id" in datasheets.
3. Pick one that can handle the voltage levels you will require (12V). This means that the maximum "gate-to-source voltage" (Vgs) and the "drain-to-source breakdown voltage" (Vdss normally) BOTH need to be at least 15V.
4. Make sure that the threshold voltage will work. The threshold voltage is the exact voltage between the gate and the source where the MOSFET switches between "OPEN" and "CLOSED". Typically, this is around 1V. You need it to be somewhere between 0V and 12V.
Just to point you in the right direction, take a look at International Rectifier's IRF1503. It should be able to handle just about anything you could throw at it. I'd order from Digikey.
So, just to recap where we're at, we now have the two LEDs flashing continuously and in sync at a frequency that we can control with a potentiometer. Now we need to get them to only flash sometimes.
DPDT Switches
A DPDT switch has two throws, which move in tandem, each between its own two poles. Instead of trying to explain why I designed the switch setup the way I did, I'll just walk you through the circuit behavior.
If DPDT#1 is in its current position, there would be no positive voltage connected to the astable multivibrator, meaning that it would not be outputting its flashing waveform. Additionally, the D terminal of MOSFET #1 would be connected to ground, applying +12V directly to the LED module. Therefore, LED #1 would be on continuously.
If DPDT#1 switches to its other position, +12V would be applied to the astable multivibrator, causing it to power on and output the flashing waveform to both of the MOSFETs. If DPDT #2 were in its current position, LED#2 would still be on continuously (D term. of MOSFET #2 connected to GND). However, because the D terminal of MOSFET #1 is not grounded any longer, LED #1 would flash on and off in time with the output from the astable multivibrator.
---------------------------------------------
So... that's it, really. Two independently-controlled turn signals. And it only took 2 types of IC's! If you decide to give this or something like it a try, feel free to post questions. Good luck!
-Likearock
I figured that posting an easy how-to for the electronics behind making your own LED turn signals might be helpful to some people. I'm trying to make this post a good balance between simple, educational, and fun to build. To all you Electrical Engineering buffs out there, be forewarned that the circuit I drew up to share is a little overly simplistic (couple optional resistors missing, etc.), but it will work just fine for our purposes. Also, I'd just like to say that this is pretty basic and has probably all been done before by someone else, so I'd just like to let you know that it's not very original. But it does work great!
Hope someone can get some benefit out of this! Feel free to question away.
---------------------------------------------
How to Build your own LED Turn Signals
You will need:
- 2x medium-sized 12V LED modules. I got mine at AutoZone (kind of like this one), but you can find them all over the net. What you're looking for is a red or yellow housing that contains maybe 5-10 LEDs. There should be 2 wires sticking out of it. Just about any type that fit this description will work.
- A means for powering your LEDs. For this how-to, I'm assuming that you have a 12V SLA battery like I do. This setup should also work for 6V systems, although I've not tried a "white wire" setup before.
- 2x N-channel MOSFETS with sufficient current and voltage capabilities. I used International Rectifier's IRLML2803 (datasheet here), but I wouldn't recommend them, for reasons I'll explain later. If you don't know what MOSFETs are, don't worry. We'll get to that later, and they're easy to work with - I promise.
- 1x astable multivibrator or oscillator. I used Texas Instruments' CD4047BE in astable mode (datasheet here), but a standard 555 timer could also be modified to fit the system. Again, don't let the terminology freak you out. We'll clear all this up in a bit.
- Wire, solder, soldering iron, multimeter.
- 2x Dual-pole, Dual-throw switches, one resistor, and one capacitor (details below). RadioShack has them.
------------
So, I guess now would be the time to dive in. First of all, let's think about what we're trying to do. What I was shooting for were two tail lights that, when connected to the battery, were always on, except when I wanted to turn. When turning, I wanted to be able to flip a switch and have one of the two lights go from always on to flashing.
That means that we need to be applying 12V to each of the LEDs continuously, then throw a switch and apply 12V to one of the LEDs intermittently and the other continuously.
So how can you do this? Well, imagine two parallel ways of powering the LEDs. One way is 12V constant, and the other way is 12V/0V intermittently. The switch changes which of the two powering methods the LED is connected to. Now would be a good time to bring up the circuit.
Astable Multivibrator
In the lower left part of the circuit diagram, there is a block (an "integrated circuit") in the lower left labeled "CD4047BE". It's called a "multivibrator," and it is currently set up to run in "astable" mode. Now, this is really just a bunch of fancy-schmancy lingo that EE's came up with to make their jobs sound complicated
So what determines how fast the voltage goes back and forth? Well, basically, there are two circuit components - a resistor (actually a potentiometer in the diagram) and a capacitor - that determine the frequency at which the voltage at pin 10 goes back and forth. The capacitor is going between pins 1 and 3, and the potentiometer is going between pins 2 and 3 in the diagram.
So how do you actually control the flashing frequency? Well, resistors and capacitors have certain values associated with them that quantify how they will behave if you put them in a circuit. Let's say that R = resistance and C = capacitance. In order to get a certain flashing frequency, you need 1/(R*C) to be, say, F (for frequency). You could have R be really big and C be really small, R be really small and C be really big, or R and C both be medium-sized, and you could get the exact same F. Therefore, the way the diagram is set up, you can vary R from very small (a few ohms) to somewhat large (3 kilo-ohms), and C is fixed at 100 uF. This allows you to dial the frequency value in by changing the R through twisting the knob on the potentiometer. For you circuits-minded people out there, this is on page 3-135 of the CD4047BE datasheet linked to above.
The other two most important pins on this integrated circuit are pins 7 and 14. 7 is where you attach 0V (GND), and 14 is where you connect +V (12V in this case).
CD4047BE Pin Recap
Pins 1-3: Attach resistor/capacitor to determine flashing frequency
Pins 4-6: Connect to V+, to "tell" the IC you want it to run in astable mode
Pin 7: This is the GND pin of the IC, where you should connect 0V
Pins 8-9: Connect to GND to "tell" the IC you want it to run in astable mode
Pin 10: This is the output of the chip, going back and forth between 0V and 12 V
Pin 11: Do nothing
Pin 12: Connect to GND to "tell" the IC you want it to run in astable mode
Pin 13: Do nothing
Pin 14: This is the V+ pin, where you should connect 12V
I get all of my circuit components from Digikey or Jameco. I provided Digikey links above.
LED Current Draw
You may be wondering why, now that we have a component that will output a flashing 12V/0V/12V/0V signal, we don't just hook 'er up to the LEDs and go. Well, as it turns out, the astable multivibrator isn't capable of actually powering the LEDs directly. In circuit-speak, the astable multivibrator isn't capable of sourcing enough current to operate the LEDs, even though its output voltage is just right.
Now I'm sure you're thinking, "So HOW much current do you actually NEED to power the LEDs?" Good question.
First, put your multimeter on the "mA DC" or "A DC" setting. To be safe, start with the highest current setting your multimeter has and work your way down. Also, be sure your multimeter probes are plugged into the correct holes (this is really easy to switch up). Black goes into "COM" or "GND", and red goes into "mA" or "A".
Next, attach the red wire (or positive lead) of your LED module to the red (+12V) terminal of the battery. Attach the black wire (or negative lead) of your LED module to the red probe of your multimeter. Attach the black probe of your multimeter to the black (0V) terminal of the battery. Your LED should light up, and your multimeter should be displaying the amount of current going through it. This is the amount of current you should pay attention to when selecting your MOSFETs. Mine turned out to be 60 mA for each of the two 5-LED light modules I went with.
N-Channel MOSFETs
So what the heck is an N-channel MOSFET? Well, for the sake of this project, its just a glorified switch. That's it. I swear. The only thing special about this switch is that instead of controlling it with a physical lever or pushbutton, you can control it with voltage! So, if you give it a high voltage (but not toooo high), it "closes the connection" (current can flow through it freely), and if you give it a voltage right around 0V (GND), it "opens the connection" (no current can flow through it). Unlike a relay, nothing mechanically opens and closes. Instead, the voltage applied to it changes the conduction properties of the materials inside. No moving parts? Even better!
Because we can control this "switch" with a voltage, we will use the output of the astable multivibrator mentioned previously to control its operation!
A MOSFET has three connections (terminals): a Gate, Drain, and Source (labeled with G, D, and S in the diagram). The gate is the pin where you apply a voltage to control the switch. As a result, we'll eventually hook pin 10 of the astable multivibrator directly to the gate of both MOSFETs (<EE's grit teeth in anguish>
As I said earlier, I picked International Rectifier's IRLML2803, due to availability. I wouldn't recommend this particular MOSFET to anyone, because it is a surface mount component (basically, it's super-tiny and kind of hard to hand-solder to without good equipment). Therefore, you'll need to pick yourself out a couple. Here is what to look for:
1. Get one in a nice big package. Any of the through-hole form factors listed on this website (down at the bottom) should work great for you. This will make soldering sooo much easier!
2. Pick one that can handle the current levels you need. Remember that LED module current measurement we did earlier? That's the one. Your MOSFET needs to be able to have a "continuous drain current" of at least 120% of the measured current. This is often labeled as "Id" in datasheets.
3. Pick one that can handle the voltage levels you will require (12V). This means that the maximum "gate-to-source voltage" (Vgs) and the "drain-to-source breakdown voltage" (Vdss normally) BOTH need to be at least 15V.
4. Make sure that the threshold voltage will work. The threshold voltage is the exact voltage between the gate and the source where the MOSFET switches between "OPEN" and "CLOSED". Typically, this is around 1V. You need it to be somewhere between 0V and 12V.
Just to point you in the right direction, take a look at International Rectifier's IRF1503. It should be able to handle just about anything you could throw at it. I'd order from Digikey.
So, just to recap where we're at, we now have the two LEDs flashing continuously and in sync at a frequency that we can control with a potentiometer. Now we need to get them to only flash sometimes.
DPDT Switches
A DPDT switch has two throws, which move in tandem, each between its own two poles. Instead of trying to explain why I designed the switch setup the way I did, I'll just walk you through the circuit behavior.
If DPDT#1 is in its current position, there would be no positive voltage connected to the astable multivibrator, meaning that it would not be outputting its flashing waveform. Additionally, the D terminal of MOSFET #1 would be connected to ground, applying +12V directly to the LED module. Therefore, LED #1 would be on continuously.
If DPDT#1 switches to its other position, +12V would be applied to the astable multivibrator, causing it to power on and output the flashing waveform to both of the MOSFETs. If DPDT #2 were in its current position, LED#2 would still be on continuously (D term. of MOSFET #2 connected to GND). However, because the D terminal of MOSFET #1 is not grounded any longer, LED #1 would flash on and off in time with the output from the astable multivibrator.
---------------------------------------------
So... that's it, really. Two independently-controlled turn signals. And it only took 2 types of IC's! If you decide to give this or something like it a try, feel free to post questions. Good luck!
-Likearock
Last edited by a moderator: